sin. x. −π2 ≤x≤π2. 2. arccos. x. 3. Statistics: 4th Order Polynomial. example. Lists: Family of sin Curves.I have a question that asks me to find an algebraic expression for sin(arccos(x)). From the lone example in the book I seen they're doing some multistep thing with the identities......we have: sin^2 theta + cos^2 theta = 1 If x in [-1, 1] and theta = arccos(x) then: theta in [0, pi] we can use the non-negative square root since we have already established that #sin(arccos(x)) >= 0#.
trigonometry - Find an algebraic expression for sin(arccos...
Didn't find what you were looking for? Ask for it or check my other videos and playlists!Постройте график функции:а) у = sin (arccos x); б) у = tg (arcctg.Популярные задачи. Тригонометрия. График sin(arccos(x)).

How do you simplify sin(arccos(x))? | Socratic
What is sin of arccos(x). Sine of arccosine of x.sin(arccosx). Выражения c функциями. Арккосинус arccos. 1/acos(x).find sin(arccos x). how do you simplify it further? This Site Might Help You. RE: sin(arccos x)? please help! this is all the question saysThe notations sin−1(x), cos−1(x), tan−1(x), etc., as introduced by John Herschel in 1813,[14][15] are often used as well in English-language sources[6]...
What is $\arccos(x)$? it is the angle given by the ratio of facets of duration $x$ and 1$. That is, on a triangle with adjacent facet length $x$ and hypotenuse duration 1$ we will be able to in finding the attitude $\arccos(x)$.
(There is a picture for this which I am hoping you can get from what I describe).
Now what is $\sin(y)$? It is the ratio of the opposite aspect to the hypotenuse of a triangle with angle $y$ in the respective phase. So if we use $y=\arccos(x)$, we've got that $\sin(y)$ is the ratio of the edges with level given by a triangle whose adjoining and hypotenuse sides are length $x$ and 1$ respectively.
Since we have the adjoining and hypotenuse lengths, we can calculate the other sides period via the Pythagorean theorem. This approach, if we use $z$ for the opposite facet, that $z^2+x^2=1^2=1$. Solving for $z$ gives $z=\sqrt1-x^2$.
Then $\sin(y)$ is the ratio of the other size, $z=\sqrt1-x^2$ and the hypotenuse, 1$. We may now say $\sin(arcos(x))=\sqrt1-x^2$.
ShowMe - arcsine,arccos,arctan

Solved: 7. Write An Algebraic Expression For Tan(arccos (x ...

`arcsin(sqrt(2x)) = arccos(sqrt(x))` Solve the equation ...
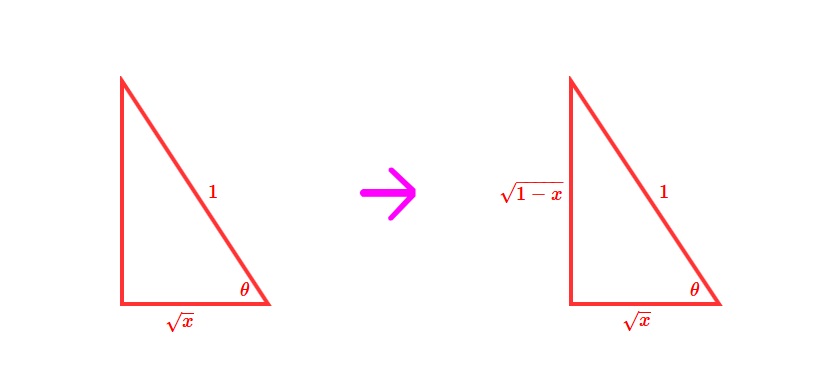
Вычислить.cos ( arccos 0, 6 )Решить уравнение cos x cos 2x ...
Solved: (1 Point) Match The Functions With Their Graphs. 1 ...

1 sin cos 3 24 1 cos sin 6 25 1 7 sin sin 4 26 arccos sin ...

Sin (arccos(0.25)) Обясните пожалуйста очень подробно ...

Simplify the expression. \sin (2 \arccos x)

sin(arcsin 1/5 + arccos x) = 1 Inverse Trigonometric ...

Could we find x in arccos x = arctan x? - Quora
Inverse Trigonometric Functions on eMathHelp

ULTRA DOMO SIN ARCOS

Inverse Trigonometric Functions (Formulas, Graphs & Problems)

Arcsin, Arccos, Arctan

Could we find x in arccos x = arctan x? - Quora
Las fotos sin ropa de Teresa Ruiz de Narcos | La Neta Noticias

Demo: sin(arccos(x)) - YouTube

How do you simplify the expression cos[arcsin(x)] * sin ...
![How do you simplify the expression cos[arcsin(x)] * sin ... How do you simplify the expression cos[arcsin(x)] * sin ...](https://i0.wp.com/useruploads.socratic.org/RijIORh9TqOwenDx1qKr_triangle.png)
sin(arcCos 0,6) Можно с маленьким объяснением)Спасибо ...

www.batmath.it di maddalena falanga e luciano battaia
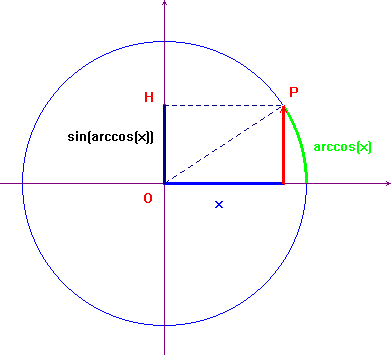
Pc 4.7 notes







No comments:
Post a Comment